各种不等式的解法收集
高中阶段各种常见的不等式的解法大收集，熟练掌握对提高运算能力有较大的帮助。
前情概要
解不等式，是高中学生的基本必修课。既能培养学生的运算能力，也能提升学生的思维能力，是学生首当其冲要过的关口。对学生的运算能力，思维能力，转化和划归能力要求较高。主要涉及从数的角度解不等式和从形的角度解不等式。
从数的角度求解
- 一元一次不等式
\(ax+b>0\)，当\(a>0\)时解集为\((-\cfrac{b}{a}，+\infty)\)；当\(a<0\)时解集为\((-\infty，-\cfrac{b}{a})\)；
- 一元二次不等式
角度一：数字系数的一元二次不等式，
①\(x^2<3\)的解集为\((-\sqrt{3}，\sqrt{3})\)，
使用方法：绝对值法，\(|x|<\sqrt{3}\)；二次函数法；穿根法，
②\(x^2+2x<0\)的解集为\((-2，0)\)
③\(-x^2+3x-2>0\)，解集为\((1，2)\)
角度二：字母系数的一元二次不等式，
如\(x^2-(a+a^2)x+a^3<0.(a\neq0)\)
- 能转化为一元二次不等式，
引例，\((x^2-3x+2)\cdot(x+1)<0\)，解集为\((-\infty，-1)\cup(1，2)\)；
引例，\(2^{x^2-x}<4\)，解集为\((-1，2)\)；
如果能理解不等式中的\(x\)的内涵，\(x\Rightarrow 代数式\)，则可以解决诸如这样的不等式，
\((2^x)^2-3\cdot 2^x+2<0\)，解集为\((0，1)\)；
\((log_2^{\;\; x})^2-3\cdot log_2^{\;\;x}+2<0\)，解集为\((2，4)\)；
- 高次不等式，可以使用转化法或穿根法
如\((3x^2-2x-1)\cdot(x^2-1)<0\)，解集为\(x\in(-1，-\cfrac{1}{3})\)；
如\((3x^2-2x-1)\cdot(x^2-1)\leq 0\)，解集为\(x\in[-1，-\cfrac{1}{3}]\cup\{1\}\)；
- 分式不等式，可以使用转化法或穿根法
如\(\cfrac{3x^2-2x-1}{x^2-1}\ge 0\)，化简为\(\cfrac{3x+1}{x+1}\ge 0\)且\(x-1\neq 0\)，故解集为\((-\infty，-1)\cup[-\cfrac{1}{3}，1)\cup(1，+\infty)\)
如\(\cfrac{2x^2+3x+1}{x-2}>0\)，解集为\(x\in(-1，-\cfrac{1}{2})\cup(2，+\infty)\)；
\(\cfrac{e^x(x+1)(2x-1)}{x^2}>0\)，解集为\(x\in(-\infty，-1)\cup(\cfrac{1}{2}，+\infty)\)；
- 绝对值不等式
由于比较难把握，故单独成篇，以期能说清楚，请参阅绝对值不等式
- 指数不等式和对数不等式
由于难度比较大，鉴于学生需要，单独成篇，请参阅 指数不等式与对数不等式
- 三角不等式
- 分段函数不等式
请参阅分段函数方程和分段函数不等式 - 静雅斋数学 - 博客园
- 抽象函数不等式
请参阅求解函数不等式| 给定抽象函数 - 静雅斋数学 - 博客园
请参阅 抽象函数不等式
-
无理不等式 求解\(2\leqslant 2\sqrt{3^2-\cfrac{|2+a|^2}{2}}\leqslant 6\)
-
排列数组合数不等式
\(\begin{cases} C_{10}^r2^{10-r} \ge C_{10}^{r-1}2^{11-r} \\ C_{10}^r2^{10-r}\ge C_{10}^{r+1}2^{9-r} \end{cases}\)
从形的角度求解
- 利用图像解不等式
分析：由三个二次的关系可知，\(f(x)<0\)的解集为\(\{x\mid 1<x<3\}\)，
故由\(f(log_2^\;x)<0\)可得，\(1<log_2^\;x<3\)，即\(log_2\;2<log_2^\;x<log_2\;8\)，故\(2<x<8\)；
- 导函数的不等式，利用形来求解能更快些
如已知函数的解析式为\(f(x)=\cfrac{2x+1}{x}\cdot e^x\)，求解单调区间，
分析：实质就是解不等式\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}>0\)和\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}<0\)，
此时可以通过穿根法解分式不等式。
\((-\infty，-1)和(\cfrac{1}{2}，+\infty)\)单调递增；\((-1，0)和(0，\cfrac{1}{2})\)单调递减；
综合转化
- 指能转化为解不等式的问题
分析：集合\(A\)为定集，集合\(B\)为动集，又因为出现了条件\(B\subseteq A\)，故需要针对集合\(B\)分类讨论如下：
1、当集合\(B=\varnothing\)时，则有\(m+1\ge 2m-1\)，解得\(m\leq 2\)；
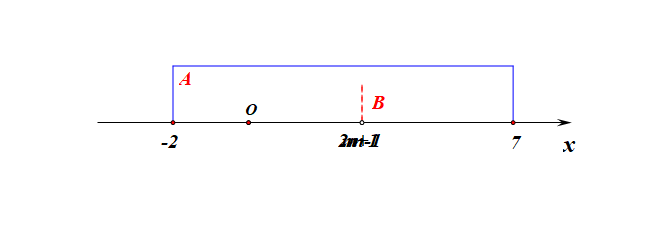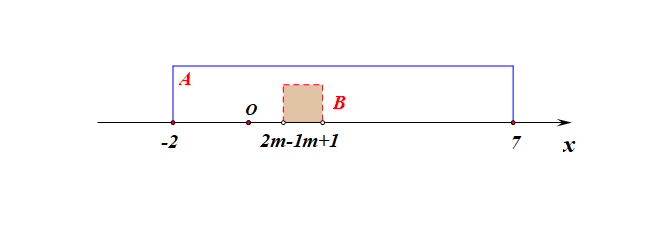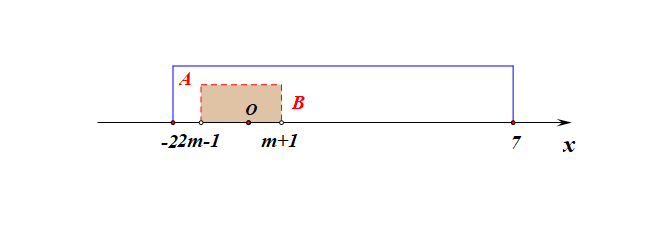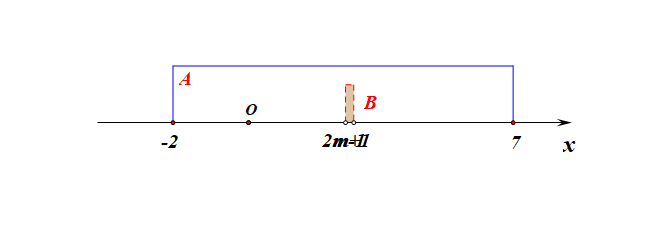
2、当集合\(B\neq\varnothing\)时，必须满足三个条件，即\(\begin{cases}&m+1<2m-1\\&-2\leq m+1\\&2m-1\leq 7\end{cases}\)，解得\(2<m\leq 4\)；
综上所述：实数\(m\)的取值范围是\(\{m\mid m\leq 4\}\)。
分析：自行画出草图可知，若存在满足题意的实数\(m\)，则必满足条件\(\begin{cases}&m+1< -2\\&2m-1> 7\end{cases}\)，解得\(m\in \varnothing\)。故这样的实数不存在。
分析：自行画出草图可知，先列出条件\(\begin{cases}&m+1\leq-2\\&1-2m \ge 7\end{cases}\)，解得\(m\leq -3\)，接下来验证\(m=-3\)是否满足题意。
当\(m=-3\)时，\(A=[-2，7]\)，\(B=[m+1，1-2m]=[-2，7]\)，此时\(A=B\)，不满足题意，舍去，故实数\(m\)的取值范围为\(\{m\mid m<-3\}\)。
分析：函数\(f(x)\)开口向下，对称轴是\(x=a\)，必须满足\(a\leq 1\)；函数\(g(x)\)是指数型函数，必须满足\(a+1>0\)且\(a+1\neq 1\)且\(a+1>1\)，求交集得到\(0<a\leq 1\).
分析：自行作图，结合分段函数\(f(x)\)的大致图像可知，\(f(x)\)在\(R\)上单调递增，故由\(f(2-a^2)>f(a)\)，可直接脱掉符号\(f\)，得到\(2-a^2>a\)，解得\(-2<a<1\).
(1).若函数\(f(x)\)在\(x=-1\)处取到极值\(\cfrac{1}{e}\)，试求函数\(f(x)\)的解析式和单调区间；
解析：\(f(x)=\cfrac{ax+b}{x}\cdot e^x\)，由\(f(-1)=\cfrac{1}{e}\)，
得到\(f(-1)=\cfrac{-a+b}{-1}\cdot e^{-1}=\cfrac{1}{e}\)，即\(a-b=1①\)
又\(f'(x)=(\cfrac{ax+b}{x})'\cdot e^x+\cfrac{ax+b}{x}\cdot e^x=\cfrac{ax-ax-b}{x^2}\cdot e^x+\cfrac{ax+b}{x^2}\cdot e^x\cdot x\)
即\(f'(x)=e^x\cdot \cfrac{ax^2+bx-b}{x^2}\)，由\(f'(-1)=0\)，得到\(a-2b=0②\)，
联立①②两式得到，\(\left\{\begin{array}{l}{a-b=1}\\{a-2b=0}\end{array}\right.\)，求得\(a=2，b=1\)；
则函数的解析式为\(f(x)=\cfrac{2x+1}{x}\cdot e^x\)；
求解单调区间，实质就是解不等式\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}>0\)\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}<0\)，
此时可以通过穿根法解分式不等式。
\((-\infty，-1)和(\cfrac{1}{2}，+\infty)\)单调递增；\((-1，0)和(0，\cfrac{1}{2})\)单调递减；
延伸阅读
1、穿根法的前世今生
2、三角不等式的解法
3、双连不等式
法1：自己作图如右，读图即可解答，解集为\((-1，0)\cup(1，3)\)；
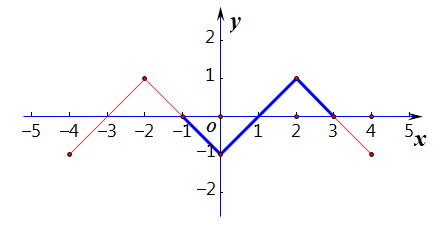
法2：利用积的符号法则求解，原不等式等价于\(\begin{cases}x>0\\f(x)>0\end{cases}\)或\(\begin{cases}x<0\\f(x)<0\end{cases}\)，
解关于\(x\)的不等式\(lnx>1-x\)；
分析：你应该能感觉到，这个题目用我们平常的那种解法(代数解法)已经不能做出来了，因为它不是我们熟悉的那种代数不等式，而是超越不等式，这时候就需要我们借助图像来求解。
比如分别作出两个函数\(y=lnx\)和\(y=1-x\)的图像观察求解，如右图所示，解集为\((1，+\infty)\)；
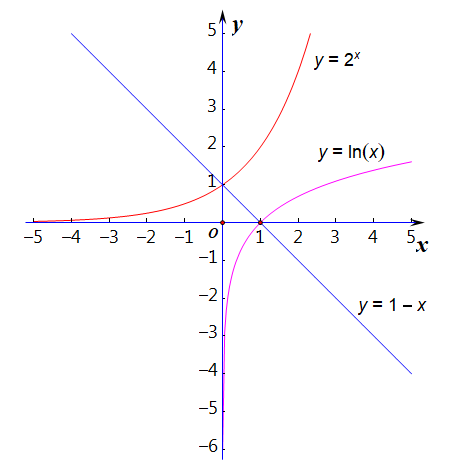
同类题目：解关于\(x\)的不等式\(2^x>1-x\)；解集为\((0，+\infty)\)；：解关于\(x\)的不等式\(log_2^x>\cfrac{2}{x}\)；解集为\((2，+\infty)\)； ↩︎
